The second law of thermodynamics states that the universe (i.e. all systems) tend to the greatest degree of randomization. This concept is defined by the term entropy, S.

S = klnW

where k = Boltzmann constant (the gas constant, R, divided by Avagadros’ number) and W = the number of substrates. For an isothermal reversible reaction the change in entropy can be reduced to the term:

ΔS = ΔH/T

Whereas, enthalpy is a term whose value is largely dependent upon electronic internal energies, entropy values are dependent upon translational, vibrational and rotational internal energies. Entropy also differs from enthalpy in that the values of enthalpy that indicate favored reactions are negative and the values of entropy are positive. Together the terms enthalpy and entropy demonstrate that a system tends toward the highest entropy and the lowest enthalpy.

In order to effectively evaluate the course (spontaneity or lack there of) of a reaction and taking into account both the first and second laws of thermodynamics, Josiah Gibbs defined the term, free energy which is defined as:

ΔG = ΔH – TΔS

Free energy is a valuable concept because it allows one to determine whether a reaction will proceed and allows one to calculate the equilibrium constant of the reaction which defines the extent to which a reaction can proceed. The discussion above indicated that a decrease in energy, a negative ΔH, and an increase in entropy, a positive ΔS, are indicative of favorable reactions. These terms would, therefore, make ΔG a negative value. Reactions with negative ΔG values are termed exergonic and those with positive ΔG values endergonic. However, when a system is at equilibrium:

ΔG = 0

Gibbs’ free energy calculations allows one to determine whether a given reaction will be thermodynamically favorable. The sign of ΔG states that a reaction as written or its reverse process is the favorable step. If ΔG is negative then the forward reaction is favored and visa versa for ΔG values that are calculated to be positive.

Standard State Conditions in Biological Reactions

To effectively interpret the course of a reaction in the presence of a mixture of components, such as in the cell, one needs to account for the free energies of the contributing components. This is accomplished by calculating total free energy which is comprised of the individual free energies. In order to carry out these calculations one needs to have a reference state from which to calculate free energies. This reference state, termed the standard state, is chosen to be the condition where each component in a reaction is at 1M. Standard state free energies are given the symbol: G°.

The partial molar free energy of any component of the reaction is related to the standard free energy by the following:

G = G° + RTln[X]

From this equation one can see that when the component X, or any other component, is at 1M the ln[1] term will become zero and:

G = G°

The utility of free energy calculations can be demonstrated in a consideration of the diffusion of a substance across a membrane. The calculation needs to take into account the changes in the concentration of the substance on either side of the membrane. This means that there will be a ΔG term for both chambers and, therefore, the total free energy change is the sum of the ΔG values for each chamber:

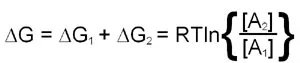
This last equation indicates that if [A]₂ is less than [A]₁ the value of ΔG will be negative and transfer from region 1 to 2 is favored. Conversely if [A]₂ is greater than [A]₁ ΔG will be positive and transfer from region 1 to 2 is not favorable, the reverse direction will be.

One can expand upon this theme when dealing with chemical reactions. It is apparent from the derivation of ΔG values for a given reaction that one can utilize this value to determine the equilibrium constant, K_eq. As for the example above dealing with transport across a membrane, calculation of the total free energy of a reaction includes the free energies of the reactants and products:

ΔG = G_(products) – G_(reactants)

Since this calculation involves partial molar free energies the ΔG° terms of all the reactants and products are included. The end result of the reduction of all the terms in the equation is:

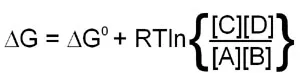
When the above equation is used for a reaction that is at equilibrium the concentration values of A, B, C and D will all be equilibrium concentrations and, therefore, will be equal to K_eq. Also, when at equilibrium ΔG = 0 and therefore:

0 = ΔG° + RTlnK_eq

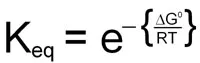
This demonstrates the relationship between the free energy values and the equilibrium constants for any reaction